DIBUJOS

http://www.speedyshare.com/files/19478638/cono_argolla1.dwg

Matlab simulador

Matlab

Simulador de secciones cónicas utilizando Microsoft Excel y MatLab 5.3

Descripción:

Aplicaciones que mediante la lectura de los coeficientes de una ecuación general de una sección cónica (parábola, elipse, hipérbola o circunferencia), muestra la gráfica y los elementos correspondientes a ésta.

MATLAB (abreviatura de MATrix LABoratory, "laboratorio de matrices") es un software matemático que ofrece un entorno de desarrollo integrado (IDE) con un lenguaje de programación propio (lenguaje M). Está disponible para las plataformas Unix, Windows y Apple Mac OS X.

Entre sus prestaciones básicas se hallan: la manipulación de matrices, la representación de datos y funciones, la implementación de algoritmos, la creación de interfaces de usuario (GUI) y la comunicación con programas en otros lenguajes y con otros dispositivos hardware. El paquete MATLAB dispone de dos herramientas adicionales que expanden sus prestaciones, a saber, Simulink (plataforma de simulación multidominio) y GUIDE (editor de interfaces de usuario - GUI). Además, se pueden ampliar las capacidades de MATLAB con las cajas de herramientas (toolboxes); y las de Simulink con los paquetes de bloques (blocksets).

Es un software muy usado en universidades y centros de investigación y desarrollo. En los últimos años ha aumentado el número de prestaciones, como la de programar directamente procesadores digitales de señal o crear código VHDL.

Historia

Fue creado por The MathWorks en 1984, surgiendo la primera versión con la idea de emplear paquetes de subrutinas escritas en Fortran en los cursos de álgebra lineal y análisis numérico, sin necesidad de escribir programas en dicho lenguaje. El lenguaje de programación M fue creado en 1970 para proporcionar un sencillo acceso al software de matrices LINPACK y EISPACK sin tener que usar Fortran.

En 2004, se estimaba que MATLAB era empleado por más de un millón de personas en ámbitos académicos y empresariales.

Sintaxis

MATLAB es un programa de cálculo numérico orientado a matrices. Por tanto, será más eficiente si se diseñan los algoritmos en términos de matrices y vectores.

Ejemplos de en Matlab

Simulación de sistemas de control continuo con Matlab y Similink

Matlab

Simulador de secciones cónicas utilizando Microsoft Excel y MatLab 5.3

Descripción:

Aplicaciones que mediante la lectura de los coeficientes de una ecuación general de una sección cónica (parábola, elipse, hipérbola o circunferencia), muestra la gráfica y los elementos correspondientes a ésta.

MATLAB (abreviatura de MATrix LABoratory, "laboratorio de matrices") es un software matemático que ofrece un entorno de desarrollo integrado (IDE) con un lenguaje de programación propio (lenguaje M). Está disponible para las plataformas Unix, Windows y Apple Mac OS X.

Entre sus prestaciones básicas se hallan: la manipulación de matrices, la representación de datos y funciones, la implementación de algoritmos, la creación de interfaces de usuario (GUI) y la comunicación con programas en otros lenguajes y con otros dispositivos hardware. El paquete MATLAB dispone de dos herramientas adicionales que expanden sus prestaciones, a saber, Simulink (plataforma de simulación multidominio) y GUIDE (editor de interfaces de usuario - GUI). Además, se pueden ampliar las capacidades de MATLAB con las cajas de herramientas (toolboxes); y las de Simulink con los paquetes de bloques (blocksets).

Es un software muy usado en universidades y centros de investigación y desarrollo. En los últimos años ha aumentado el número de prestaciones, como la de programar directamente procesadores digitales de señal o crear código VHDL.

Historia

Fue creado por The MathWorks en 1984, surgiendo la primera versión con la idea de emplear paquetes de subrutinas escritas en Fortran en los cursos de álgebra lineal y análisis numérico, sin necesidad de escribir programas en dicho lenguaje. El lenguaje de programación M fue creado en 1970 para proporcionar un sencillo acceso al software de matrices LINPACK y EISPACK sin tener que usar Fortran.

En 2004, se estimaba que MATLAB era empleado por más de un millón de personas en ámbitos académicos y empresariales.

Sintaxis

MATLAB es un programa de cálculo numérico orientado a matrices. Por tanto, será más eficiente si se diseñan los algoritmos en términos de matrices y vectores.

Ejemplos de en Matlab

Simulación de sistemas de control continuo con Matlab y Similink

Mercedes Lisstte Miranda Morales

Prueba de Turing

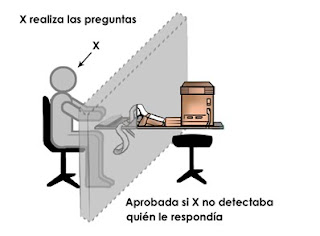
Prueba de Turing

El Test de Turing (o Prueba de Turing) es una prueba propuesta por Alan Turing para demostrar la existencia de inteligencia en una máquina. Fue expuesto en 1950 en un artículo (Computing machinery and intelligence) para la revista Mind, y sigue siendo uno de los mejores métodos para los defensores de la Inteligencia Artificial. Se fundamenta en la hipótesis positivista de que, si una máquina se comporta en todos los aspectos como inteligente, entonces debe ser inteligente.
La prueba consiste en un desafío. Se supone un juez situado en una habitación, y una máquina y un ser humano en otras. El juez debe descubrir cuál es el ser humano y cuál es la máquina, estándoles a los dos permitido mentir al contestar por escrito las preguntas que el juez les hiciera. La tesis de Turing es que si ambos jugadores eran suficientemente hábiles, el juez no podría distinguir quién era el ser humano y quién la máquina. Todavía ninguna máquina puede pasar este examen en una experiencia con método científico.
En 1990 se inició un concurso, el Premio Loebner, una competición de carácter anual entre programas de ordenador que sigue el estándar establecido en la prueba de Turing. Un juez humano se enfrenta a dos pantallas de ordenador, una de ellas que se encuentra bajo el control de un ordenador, y la otra bajo el control de un humano. El juez plantea preguntas a las dos pantallas y recibe respuestas. El premio está dotado con 100.000 dólares estadounidenses para el programa que pase el test, y un premio de consolación para el mejor programa anual. Todavía no ha sido otorgado el premio principal.

Aplicaciones
Una de las aplicaciones de la prueba de Turing es el control de spam. Dado el gran volumen de correos electrónicos enviados, el spam es, por lo general, enviado automáticamente por una máquina. Así la prueba de Turing puede usarse para distinguir si el correo electrónico era enviado por un remitente humano o por una máquina (por ejemplo por la prueba Captcha).
Captcha
Captcha es el acrónimo de Completely Automated Public Turing test to tell Computers and Humans Apart (Prueba de Turing pública y automática para diferenciar máquinas y humanos).


Características
El sistema captcha tiene las siguientes características por definición:
• Son completamente automatizados, es decir, no es necesario ningún tipo de mantenimiento / intervención humana para su realización. Esto supone grandes beneficios en cuanto a fiabilidad y coste.
• El algoritmo utilizado es público. De esta forma la ruptura de un captcha pasa a ser un problema de inteligencia artificial y no la ruptura de un algoritmo secreto.

Turing y Matlab

Download Prueba de Turing.pdf for free on uploading.com

TEST

Matlab

http://www.speedyshare.com/files/19346403/Traba_MATLAB.pdf

Video

[basq]

caja

Download Universidad Politécnica de Nicaragua.pdf for free on uploading.com

Moneda

aqui link de descarga
http://uploading.com/files/48ede8mc/Universidad%2BPolit%25C3%25A9cnica%2Bde%2BNicaragua.pdf/

metodologia del desarrollo de un modelo

La simulación como tal es un proceso y en general consta de las siguientes etapas.

• Definición del sistema:

Para tener una definición exacta del sistema que se desea simular, es necesario hacer primeramente un análisis preliminar de éste, con el fin de determinar la interacción con otros sistemas, las restricciones del sistema, las variables que interactúan dentro del sistema y sus interrelaciones, las medidas de efectividad que se van a utilizar para definir y estudiar el sistema y los resultados que se esperan obtener del estudio.

• Formulación del modelo :

Una vez definidos con exactitud los resultados que se esperan obtener del estudio, se define y construye el modelo con el cual se obtendrán los resultados deseados. En la formulación del modelo es necesario definir todas las variables que forman parte de él, sus relaciones lógicas y los diagramas de flujo que describan en forma completa el modelo.

• Colección de datos :

Es importante que se definan con claridad y exactitud los datos que el modelo va a requerir para producir los resultados deseados.

• Implementación del modelo en la computadora :

Con el modelo definido, el siguiente paso es decidir si se utiliza algún lenguaje como el fortran, algol, lisp, etc., o se utiliza algún paquete como Vensim, Stella y iThink, GPSS, simula, simscript, Rockwell Arena etc., para procesarlo en la computadora y obtener los resultados deseados.

• Validación :

A través de esta etapa es posible detallar deficiencias en la formulación del modelo o en los datos alimentados al modelo. Las formas más comunes de validar un modelo son:

1. La opinión de expertos sobre los resultados de la simulación. 2. La exactitud con que se predicen datos históricos. 3. La exactitud en la predicción del futuro. 4. La comprobación de falla del modelo de simulación al utilizar datos que hacen fallar al sistema real. 5. La aceptación y confianza en el modelo de la persona que hará uso de los resultados que arroje el experimento de simulación.

• Experimentación :

La experimentación con el modelo se realiza después que éste haya sido validado. La experimentación consiste en generar los datos deseados y en realizar un análisis de sensibilidad de los índices requeridos.

• Interpretación :

En esta etapa del estudio, se interpretan los resultados que arroja la simulación y con base a esto se toma una decisión. Es obvio que los resultados que se obtienen de un estudio de simulación ayuda a soportar decisiones del tipo semi-estructurado.

• Documentación :

Dos tipos de documentación son requeridos para hacer un mejor uso del modelo de simulación. La primera se refiere a la documentación del tipo técnico y la segunda se refiere al manual del usuario, con el cual se facilita la interacción y el uso del modelo desarrollado.

Modelo Lineal General

En el caso estudiado, la variable de respuesta es el logaritmo de la carga viral.

Vonesh y Chinchilli (1997) proponen un modelo de ensayo clínico de medidas repetidas basado en una modificación del modelo clásico de medidas repetidas de efectos fijos al que se ha incorporado efectos aleatorios univariantes:

logCVijk = m + ti + dj(i) + Vk + (tV)ik+ eijk (1)

Donde

logCVijk = Logaritmo de la carga viral para individuo i, tratamiento j y

visita k.

m = media general

ti = efecto fijo del tratamiento i

Vk = efecto fijo de la visita k..

(tV)ik = efecto fijo del tratamiento i y de la visita k.

dj(i) = efecto aleatorio del paciente j en el tratamiento i.

eijk = error aleatorio.

Se asume que eijk y dj(i) son independientes y se distribuyen según eijk

~N(0,s2

e), dj(i) ~N(0,s2

d). Mediante la transformación descrita en Vonesh y Chinchilli (1997) se obtiene como resultando un modelo más interpretable y sencillo de simular:

logCV*ijk = V*k + (tV)*ik+ e*ijk (2)

Equivalente a (1), donde,

V*k = efecto fijo de la visita k.

(tV)*ik = efecto de la interacción entre el tratamiento i de la visita k

e*ijk = error aleatorio.

El principal inconveniente del modelo (2) (ó 1) es su excesiva parametrización (p.e. es necesario estimar un parámetro para describir el efecto de cada instante de visita), con los consiguientes problemas de inferencia simultánea. Tampoco representa de una manera natural la heterogeneidad en las respuestas individuales. Estos defectos están en gran parte paliados bajo un enfoque de modelos mixtos.

Modelo Lineal Mixto

El modelo lineal mixto se puede plantear, en términos generales (véase, por ejemplo, Verbeke y Molenberghs, 2001) de la siguiente forma:}

Yi = Xib + Zibi + ei (3)

Donde Yi es el vector de observaciones correspondiente al individuo i, Xi y Zi son matrices de diseño, b es un vector de parámetros fijos, b~N(0,D) es un vector de parámetros aleatorios, ei ~N(0,åi) es el vector de residuos para el individuo i y b1,...,bN, e1,...,eN son independientes.

Un posible modelo para el caso estudiado es:

logCVij = (b0 + b0i) + (b1 + b1i) + (b2 + b2i) Visitaij + eij (4)

Donde:

logCVij =logaritmo de la carga viral del individuo i en la visita j,

b0, b0i = Parte fija y aleatoria de la carga viral inicial,

b1, b1i = Parte fija y aleatoria del efecto del tratamiento,

b2, b2i = Parte fija y aleatoria de efecto de la visita,

Visitaij = Tiempo (meses) desde inicio del tratamiento, y

eij = error aleatorio.

Para el análisis del modelo de medidas repetidas propuesto y la estimación de parámetros se ha empleado los procedimientos PROC MIXED de SAS. En este caso concreto la modelización y simulación de los ensayos clínicos se ha realizado también utilizando el paquete estadístico SAS 8.